Логистическая регрессия в R

Логистическая регрессия - статистическая модель, которая применяется для предсказания вероятности возникновения некоторого события по значениям множества признаков.

Модель

Обозначим предсказываемую зависимую переменную как $y$. Она может принимать два значения $0$ - событие не произошло и $1$ - событие произошло.

Вероятность того, что событие произойдет $P(y=1)$. Тогда $P(y=0)=1 - P(y=1)$ вероятность того что событие не произойдет. Используя для предсказания независимые переменные $x_1, x_2…,x_k$ получим функцию предсказания:

$$P(y=1)=\frac{1}{1+e^{-(B_0 + B_1 * x_1+B_2 * x_2+…+B_k * x_k)}}$$

Функция возвращает вероятность того, что $y=1$, т.е. событие произошло и имеет вид:

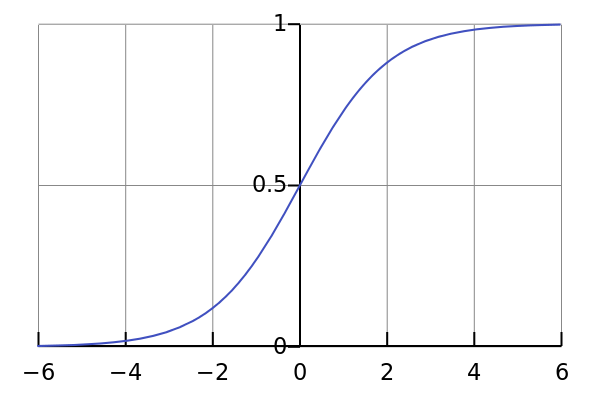
Logistinc regression sample

Логистическая регрессия в R

Построим модель предсказывающую вероятность выживания каждого пассажира на Титанике используя реальные данные (тренировочные, тестовые):

#  Загружаем данные в dataframe
setwd("path/to/working/directory")
data <- read.csv("train.csv")

#  Рассмотрим структуру данных
str(quality)

#'data.frame':   891 obs. of  12 variables:
# $ PassengerId: int  1 2 3 4 5 6 7 8 9 10 ...
# $ Survived   : int  0 1 1 1 0 0 0 0 1 1 ...
# $ Pclass     : int  3 1 3 1 3 3 1 3 3 2 ...
# $ Name       : Factor w/ 891 levels "Abbing, Mr. Anthony",..: 109 191 358 277 16 559 520 629 417 581 ...
# $ Sex        : Factor w/ 2 levels "female","male": 2 1 1 1 2 2 2 2 1 1 ...
# $ Age        : num  22 38 26 35 35 NA 54 2 27 14 ...
# $ SibSp      : int  1 1 0 1 0 0 0 3 0 1 ...
# $ Parch      : int  0 0 0 0 0 0 0 1 2 0 ...
# $ Ticket     : Factor w/ 681 levels "110152","110413",..: 524 597 670 50 473 276 86 396 345 133 ...
# $ Fare       : num  7.25 71.28 7.92 53.1 8.05 ...
# $ Cabin      : Factor w/ 148 levels "","A10","A14",..: 1 83 1 57 1 1 131 1 1 1 ...
# $ Embarked   : Factor w/ 4 levels "","C","Q","S": 4 2 4 4 4 3 4 4 4 2 ...


#  Немного очистим данные

#  Заменим строки, в которых отсутствует возраст медианой
data$Age[is.na(data$Age)] <- median(data$Age, na.rm=TRUE)

#  Создадим модель зависимости выживания пассажира от его пола,
#  класса которым он путешествует и возраста.
#  family = binomial именно этот параметр указывает что мы хотим использовать логистическую регрессию

model = glm(Survived ~ Sex + Pclass + Age, data=data, family = binomial)

#  Рассмотрим нашу модель
summary(QualityLog)

# Estimate указывает коэффициент Bi перед независимой переменной
# Количество "*" указывает на значимость переменной в модели,
# в нашем случае все независимые влияют на зависимую очень сильно

#Coefficients:
#  Estimate Std. Error z value Pr(>|z|)    
#  (Intercept)  4.724739   0.449822  10.504  < 2e-16 ***
#  Sexmale     -2.612279   0.186505 -14.006  < 2e-16 ***
#  Pclass      -1.171719   0.119318  -9.820  < 2e-16 ***
#  Age         -0.033311   0.007371  -4.519  6.2e-06 ***
#  ---
#  Signif. codes:  0 '**' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

#(Dispersion parameter for binomial family taken to be 1)

#Null deviance: 1186.66  on 890  degrees of freedom
#Residual deviance:  805.59  on 887  degrees of freedom
#AIC: 813.59

#  Загрузим тестовые данные
test <- read.csv("test.csv")

#  Используем модель для предсказаний на тестовых данных

#  predictResult содержит вектор с вероятностью выживания для каждого пассажира
predictResult <- predict(model, newdata = test, type="response")

#  Теперь в тестовой выборке значение Survived установлено в 1
#  если вероятность положительного исхода больше либо равна 50%
#  и 0 в противном случае

test$Survived[predictResult >= 0.5] = 1
test$Survived[predictResult < 0.5] = 0

# На реальных данных модель правильно предсказывает результат в 74.641% случаев.

Receiver Operator Characteristics (ROC) кривая

Результатом логистической регрессии является вероятность того что событие произойдет, но чтобы сделать предсказание нам необходимо определить пороговое (threshold) значение $t$, такое что:

При высоком пороговом значении модель редко будет предсказывать положительный результат (только при высокой вероятности $P(y=1)$). И обратно, при низком пороговом значении модель будет чаще предсказывать положительный исход и реже отрицательный.

Для численного представления качества оценки используют матрицу неточностей (confusion matrix).

Predicted = 0 Predicted = 1
Actual = 0 True Negatives (TN) False Positives (FP)
Actual = 1 False Negatives (FN) True Positives (TP)

В таблице мы видим как часто наша модель делает правильные предсказания:

И как часто ошибается:

Отсюда можно получить два значения, которые помогут нам определить какие ошибки делает модель:

$Sensitivity = TP / (TP + FN)$ - чувствительность, или True positive rate. Процент верно предсказанных позитивных исходов.

$Specificity = TN / (TN + FP)$ - специфичность или True negative rate. Процент верно предсказанных негативных исходов.

Модель с более высоким пороговым значением будет иметь более высокую чувствительность и низкую специфичность. Модель с низким пороговым значением наоборот.

Если предпочтений нет можно оставить пороговое значение $t = 0.5$.

#  Используем модель для предсказания на тестовых данных
#  для этого не указываем параметр newdata

predictTrain <- predict(model, type="response")

#  0.5 в данном случае является пороговым значением
table(data$Survived, predictTrain > 0.5)

#  Модель верно предсказывает отрицательный исход в 454 случаях из 594
#  И положительный исход в 294 случаях из 342

#    FALSE TRUE
#  0   454   95
#  1    93  249

sensitivity <- 249 / (93 + 249) #  0.7280702

specificity <- 454 / (454 + 95) #  0.8269581

Подобрать необходимое пороговое значение можно с помощью ROC-кривой.

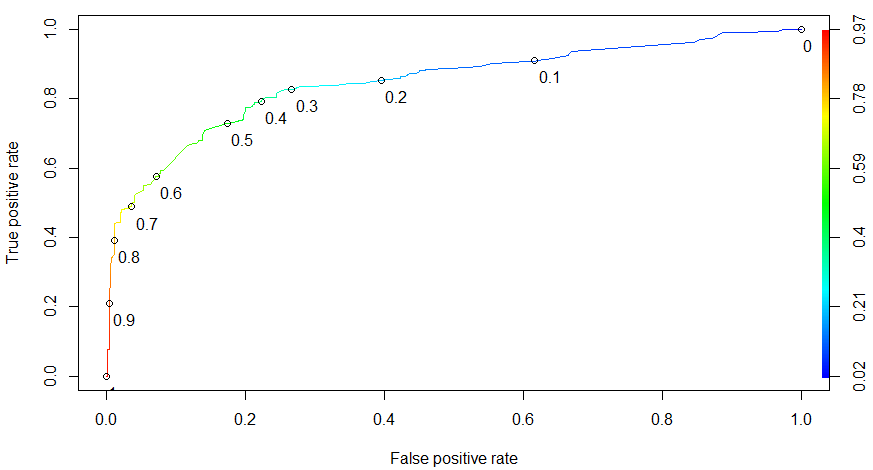
ROC Curve

True negative rate указывается на оси абсцисс, True positive rate на оси ординат. Кривая показывает соотношения этих величин при разных значения пороговой величины.

Построить ROC-кривую в R можно следующим набором команд:

# Устанавливаем необходимый пакет

install.package("ROCR")
package(ROCR)

# Строим ROC-кривую

ROCRpred = prediction(predictTrain, data$Survived)
ROCRperf = performance(ROCRpred, "tpr", "fpr")
plot(ROCRperf, colorize=TRUE, print.cutoffs.at=seq(0,1,0.1), text.adj=c(-0.2,1.7))